The Last Word On Nothing

“The most distinct and beautiful statement of any truth must take at last the mathematical form.” —Henry David Thoreau

April is Mathematics Awareness Month. April is also National Poetry Month. Coincidence? Yep, almost definitely. But it’s also an opportunity: I’d like to propose that we—you and I, at least until the end of this blog post—merge the two and celebrate the first-ever Mathematical Poetry Month. No fooling.

Connecting math to poetry isn’t a new idea. Archimedes did it, committing the mother of all word problems—a Diophantine beast—to verse. The Sator Square, a mysterious Latin palindrome written in a square that can be read in multiple directions, is a pattern poem with mathematical underpinnings. (The oldest-known Sator Square was recovered from Pompeii. The one pictured here contains the same words, but was found in France.)

In a letter to his brother dated March 31, 1791, Samuel Taylor Coleridge called math the “quintessence of truth.” As a demonstration of his enthusiasm for said quintessence, he declared his intention to refashion Euclid’s Elements, which contained most of those propositions and proofs we met in school, as a series of Pindaric odes. The letter even included his first stab at versifying the first of Euclid’s propositions. As far as anyone knows, that’s as far as he got. (Read Coleridge’s letter here. Did he improve on Euclid?) One of the most famous pieces by the American poet Edna St. Vincent Millay, similarly besotted by the great Greek, is “Euclid alone has looked on beauty bare.”

Other famous mathematical ideas have also made it into poems and songs. Tom Apostol penned and sung “Where are the zeros of zeta of s?”, a reference to the Riemann Hypothesis, a conjecture that has resisted proof for more than 150 years. (Got an idea? A solution will net you $1 million.) Folk musician Lucy Kaplansky performs “A Song about Pi,” a jazzy song penned by her mathematician father Irving. And no, it doesn’t go on forever.

Diane Ackerman (“…the world is all subtraction in the end.”), Langston Hughes, Carl Sandburg, Wisława Szymborska, Octavio Paz, and Pablo Neruda borrowed the trappings of mathematics in their poems. Then there’s Oulipo, or the Workshop of Potential Literature, a whole group of math-crazed poets founded in 1960 by a French poet and a French mathematician. They established formulas for constructing poems, maintaining that an endless supply of profound verses could blossom from such strict confines. (Search “Hundred Thousand Billion Poems” for more on that.)

The theorems, proofs, and equations of mathematics are Big Ideas distilled to their naked cores. And what’s a poem, if not the pure distillation of an experience, emotion or idea? The reach of mathematics—its infinities, its transcendental numbers, its Hairy Ball Theorem—far exceeds the material grasp of the boring old real world. Its language seems to speak to a spooky-but-elemental otherworld, which might help explain its appeal to poets.

That “spooky otherworld” quality might also explain the ubiquity of the complaint that most of us will never, ever, ever need the quadratic formula, or the fundamental theorem of calculus, or fractals, in our entire lives.

The field of mathematical poetry isn’t without its own contretemps. The community is divided—though by a gentle, friendly divide, more rolling valley than Grand Canyon—over the very term “mathematical poetry.” Many poets dislike the term because it’s ill-defined. People disagree on what constitutes a math poem; for a list of definitions and opinions on the matter, see this 2010 post on the blog of engineer and poet Kaz Maslanka. (And see Maslanka’s blogroll if you’re looking for a new rabbit hole to fall into.)

It’s an interesting question: What makes a poem “mathematical”? Does it require addition? Derivatives? A prime number of syllables in every line? What if line lengths are based on numbers in the Fibonacci sequence, as in the case of the brief Internet craze for “Fibs”? Are those math poems?

Some practitioners posit that a mathematical poem needs a direct connection, like the simple and elegant “Addition” by Langston Hughes, or this piece by Randall Munroe, the genius behind xkcd:

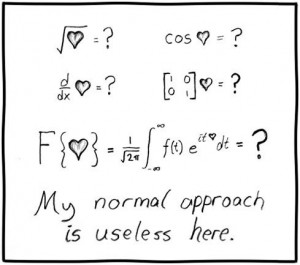
Or the following beauty, “Sacrifice and Bliss” by Kaz Maslanka:

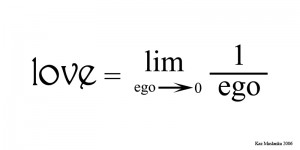
(Please note: The genre isn’t limited to beautiful expressions. My inner seventh grader just asked me to inform you that we have not even mentioned dirty mathematical limericks. I’ll leave you to Google those yourself.)

I don’t know if the field of mathematical poetry is growing, or if it’s a case of once-you-hear-about-it-you-find-it-everywhere. (My wife and I, for reasons we don’t remember, call this “the pterodactyl effect.”) But I do know there were mathematical poetry sessions at the Joint Mathematics Meeting in Baltimore in January, and also at last year’s Bridges conference in New York. The Journal of Humanistic Mathematics includes a poem in every issue. I think mathematical poetry is more than just a literary party trick: Math can propel a poem into an interesting and surprising place. That said, I don’t know if the reverse is true because I’ve yet to interview a mathematician who cited a poem as inspiration, but that doesn’t mean they’re not out there. 

So this month, let’s hear it for the math poets. Please raise your glasses! But don’t, as the mathematicians warn, drink and derive.

__________

For an excellent overview of the field, see this paper—or really, almost any paper on the subject—by mathematician and poet Sarah Glaz at the University of Connecticut. Her research helped fuel both this post and a recent article I wrote for PNAS. If you’re looking for a whole book of math poems about love and love poems that employ the trappings of math, check out Strange Attractors, edited by Glaz with JoAnne Growney, a mathematician and poet who blogs about the intersection of the two fields here.

***

Stephen Ornes is a science writer and t-ball coach in Nashville. He’s the author of a young adult biography of mathematician Sophie Germain and a contributor to The Science Writers’ Handbook. 

Image credits: M Disdero via Wikipedia, xkcd.com, Kaz Maslanka